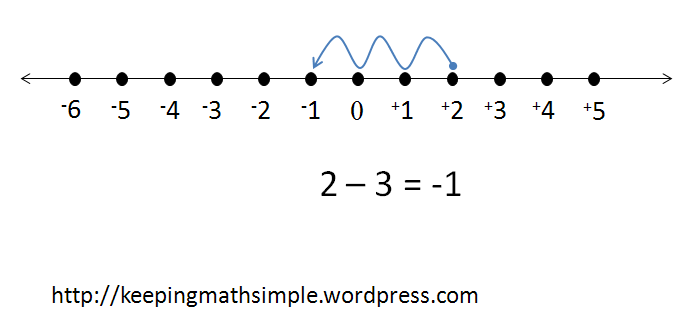
Multiplying and Dividing Positive and Negative Integers

Hello,

In our last post, we discussed how to add and subtract positive and negative integers.  Today, we are going to learn how to multiply and divide by positive and negative integers.  It is basically the same thing as multiplying and dividing normally, but we need to memorize some rules so we do not mix any signs up.

Rules to remember:

1.) Positive x positive = positive
2.) Negative x negative = positive
3.) Positive x negative = negative
4.) Negative x positive = negative
5.) Positive / positive = positive
6.) Negative / negative = positive
7.) Positive / negative = negative
8.) Negative / positive = negative

***Same sign = positive****
***Different sign = negative***

Get it? Let's practice!

Examples:

1.) (-5) x (-6) = ?
2.) (4) x (-2) = ?
3.) (9) x (9) = ?
4.) (-3) x (12) = ?
5.) (-36) / (9) = ?
6.) (80) / (-10)  = ?
7.) (-12) / (-6) = ?
8.) (56) / (7) = ?
9.) (12) x (-6) = ?
10.) (-11) / (11) = ?

Solutions:

1.) 30
2.) -8
3.) 81
4.) -36
5.) -4
6.) -8
7.) 2
8.) 8
9.) -2
10.) -1

The following links will help reiterate our lesson and will help you practice multiplying and dividing integers with negative signs:

1.) Examples and explanation with multiplying and dividing positive and negatives
2.) Practice worksheet with multiplying positive and negative integers; Answers at the bottom
3.) Practice worksheet with dividing positive and negative integers; Answers at the bottom

Adding and Subtracting Positive and Negative Integers

Hello,

We are going to move on from measurement, and we are going to learn how to add and subtract positive and negative integers.  Basically, you just need to remember some basic rules and you will be fine.  

The following are rules that you should memorize, especially when you get into more advanced math, which requires you to remember adding and subtracting positive and negative numbers very quickly:

1.) positive + positive = positive; add the two numbers like you normally would

2.) Larger positive + smaller negative = positive; subtract the two numbers like you normally would

3.) Smaller positive + larger negative = negative; subtract the two numbers like you normally would

4.) negative + negative = negative; keep the negative and add the two numbers like you normally would

5.) positive - positive = positive; subtract the two numbers like you normally would

6.) positive - negative = positive + positive = positive; just add the two numbers like you normally would

7.) negative - negative = negative or a positive depending; subtract the two numbers like you normally would 

This may look extremely confusing, but let's try some examples and hopefully it will look less confusing!

Examples:  

1.) 8 + 2 = ?

2.) 5 + (-10) = ?

3.) 4 - 9 = ?

4.) (-6) + (-6) = ?

5.) (-7) - (-3) = ?

6.) 10 - 5 = ?

7.) (-2) + 14 = ?

8.) 8 - 12 = ?

9.) 1 + (-4) = ?

10.) 3 - (7) = ?

Solutions:

1.) 8 + 2 = 10

2.) 5 + (-10) = -5 ; the larger number has the negative, so we are using rule 3 from above; we keep the negative and subtract like normal.

3.) 4 - 9 = -5 ; this can also be written as 4 + (-9) and it becomes just like number 2; we keep the negative and subtract the two.

4.) (-6) + (-6) = -12 ; when we add two negatives, we keep the negative and add the two numbers together.

5.) (-7) - (-3) = (-7) + 3 = -4 ; a minus a negative is equal to a positive, and since the negative is with our bigger number, 7, we keep the negative and subtract the two.

6.) 10 - 5 = 5

7.) (-2) + 14 = 14 - 2 = 12

8.) 8 - 12 = 8 + (-12) = - 4

9.) 1 + (-4) = -3

10.) 3 - (7) = -4 

The following are links that help reiterate our lesson, and they will also help you practice:

1.) Reiteration of our lesson, with a practice at the bottom

2.) Another reiteration of how to add and subtract positive and negative integers

3.) Example problems with adding and subtracting positive and negative integers using a number line

4.) Another practice worksheet

I hope these help!

Measurement in Terms of Volume: Metric System

Hello,

So far, we have learned units of the metric system in terms of length, including meters, millimeters, centimeters, kilometers, yards, feet, and inches.  Today, we are going to be learning units of the metric system in terms of volume.  Volume is defined as the amount of space that an object or substance takes up measured in cubic units.  The basic unit of volume is the liter, just as with length, we had the basic unit of length being the meter.

We will define 6 prefixes that contain liter, and then we will learn how to convert from each.

Prefixes of the Liter:


1.) Kiloliter ; kilo = 1000 liters
2.) Hectoliter ; hecto = 100 liters
3.) Decaliter ; deca = 10 liters
4.) Deciliter ; deci = 1/10 liters
5.) Centiliter ; centi = 1/100 liters
6.) Milliliter ; milli = 1/1000 liters

Notice the pattern above; as we move down from 1 through 6, the unit is one-tenth as large as the previous unit.  If we memorize these prefixes, it is very easy to convert from one unit to the other.  Let's practice converting each to liters and vice versa.

Examples:   


1.) 20 hectoliters = ? liters
2.) 14 kiloliters = ? liters 
3.) 4 liters = ? milliliters
4.) 32 liters = ? decaliters
5.) 2 Centiliters = ? liters
6.) 45 liters = ? milliliters 
7.) 8 deciliters = ? liters
8.) 50 kiloliters = ? liters
9.) 5 liters = ? decaliters
10.) 6 hectoliters = ? liters

Solutions:


1.) 20 hectoliters = 2000 liters ; 20 x 100 = 2000
2.) 14 kiloliters = 14000 liters ; 14 x 1000 = 14000
3.) 4 liters = 0.004 liters ; (1/1000) x 4 = 0.004
4.) 32 liters = 3.2 decaliters ; 32/10 = 3.2
5.) 2 centiliters = 0.02 liters ; (1/100) x 2 = 0.02
6.) 45 liters = 45000 milliliters ; 45/(1/1000) = 45000
7.) 8 deciliters = 0.8 liters ; (1/10) x 8 = 0.8
8.) 50 kiloliters = 50000 liters ; 50 x 1000 = 50000
9.) 5 liters = 0.5 deciliters ; 5/10 = 0.5
10.) 6 hectoliters = 600 liters ; 6 x 100 = 600

Get it? The following links will help you practice with these conversions:

1.) worksheet to help you practice converting from milliliters to liters and vice versa
2.) Answer key to worksheet 1
3.) Worksheet: a nice review of conversions involving length and volume
4.) Answer key to worksheet 2

This link below will help reiterate units of length and volume

4.) Charts for units of length and volume

This link below is meant to be fun: Metric word search =) Do not cheat and look at the answers at the bottom of the page, try it yourself first:

5.) Metric Word Search with Solutions at the Bottom of the Page

Measurement in Terms of Length: Metric System

Hello,

In our previous post we talked about measurements of the metric system in terms of length, including converting measurements to meters.  Today, we are going to learn about more units of the metric system in terms of length.  We are going to focus on inches, feet, and yards.  We are going to learn how to convert from the three.

In order to make conversions, we must note:

1.) 1 inch = 0.83333333... feet
2.) 1 inch = 0.0277777... yards
3.) 1 foot = 12 inches
4.) 1 foot = 0.333333... yards
4.) 1 yard = 36 inches
5.) 1 yard = 3 feet

Let's try some examples:

1.) 4 feet = ? inches
2.) 15 inches = ? feet
3.) 5 yards = ? feet
4.) 8 feet = ? yards
5.) 20 inches = ? yards
6.) 45 yards = ? inches
7.) 6 feet = ? inches
8.) 36 inches = ? yards
9.) 12 yards = ? feet
10.) 80 inches = ? feet

Solutions:

1.) 4 feet = 48 inches ; 4 x 12 = 48
2.) 15 inches = approximately 12.5 feet ; 15 x 0.8333333 = 12.49....
3.) 5 yards = 15 feet ; 5 x 3 = 15
4.) 8 feet = approximately 2.7 yards ; 8 x 0.33333 = 2.66....
5.) 20 inches = approximately 0.6 yards ; 20 x 0.027777 = 0.55....
6.) 45 yards = 1620 inches ; 45 x 36 = 1620
7.) 6 feet = 72 inches ; 6 x 12 = 72
8.) 36 inches = approximately 1 yard ; 36 x 0.027777 = .99....
9.) 12 yards = approximately 4 feet ; 12 x 0.33333 = 3.99....
10.) 80 inches = approximately 67 feet ; 80 x 0.83333 = 66.66....

The following links will help you practice with conversions:

1.) Practice worksheet with inches, feet, and yards: easy level
2.) Answer key to worksheet 1
3.) Worksheet 2 with inches, feet, and yards: medium level
4.) Answer key to worksheet 2

Measurement in Terms of Length: Metric System

Hello,

In our last post we learned what Fahrenheit and Celsius were.  Today, we are going to learn about the metric system and some of its prefixes.  The metric system is a system of measurement that involves decimals.  The original metric system was discovered in France around the 1790s. The metric system is usually abbreviated by SI.  In this post, we will go over some basic units of length, and how to convert units of measurement in terms of meters.  

The standard unit of length is the meter, abbreviated by m.  Other units of length include:

1.) Millimeter---> abbreviated by mm.
2.) Centimeter--->abbreviated by cm.
3.) Decimeter--->abbreviated by dm.
4.) Kilometer--->abbreviated by km.

Note:

1 millimeter = 0.001 meters; milli means thousandth
1 centimeter = 0.01 meters; centi means hundredth
1 kilometer = 1000 meters; kilo means thousand

Now, let's try converting measurements back into meters.

1.) 54.7 cm = ? m
2.) 23.8 mm = ? m
3.) 123 km = ? m

Solutions:

1.) Since 1 cm = 0.01 m, we must multiply (54.7 x 0.01) to find how many meters are in 54.7 centimeters.  54.7 x 0.01 = 0.547.  So, 54.7 cm = 0.547 m. 


2.) Since 1 mm = 0.001 m, multiply (23.8 x 0.001) to find how many meters are in 23.8 millimeters.  23.8 x 0.001 = 0.0238.  So, 23.8 mm = 0.0238 m.


3.) Since 1 km = 1000 m, multiply (123 x 1000) to find how many meters are in 123 kilometers.  123 x 1000 = 123,000.  So, 123 km = 123,000 m.  


The following are links that will help reiterate these metric units and will help you practice:


1.) This link reiterates the basic units of length
2.) Explanation of measuring length in the metric system: comes with a practice
3.) Practice worksheet with conversions
4.) Answer key to practice worksheet

I hope these links help!

Measurement: Fahrenheit and Celsius

Hello,


Today, we are going to move on from measuring time, and we are going to look at Fahrenheit and Celsius.  Fahrenheit and Celsius are temperature scales.  Gabriel Daniel was the inventor of Fahrenheit, and he discovered the mercury thermometer.  Did you know that water freezes at 32 degrees Fahrenheit and it boils at  212 degrees Fahrenheit?  We label Fahrenheit with an F and a degree symbol.  Celsius represents the temperature scale where 0 degrees is the freezing point and 100 degrees is the boiling point.  Anders Celsius invented the Celsius scale.  


We are going to practice converting Fahrenheit to Celsius and Celsius to Fahrenheit.  


In order to convert from Fahrenheit to Celsius, we must first note that there is a 180 degree difference between the Fahrenheit scale and Celsius scale.  Every degree on the Fahrenheit scale is 100/180, and if we reduce this, dividing each by 20, we get 5/9 on the Celsius scale.  To convert from Fahrenheit to Celsius, we first subtract 32 degrees from our temperature.  Second, we must multiply our answer by our 5/9 that we came up with before.     


In order to convert a temperature from Celsius to Fahrenheit, we must first note that every degree on the Celsius scale is opposite the Fahrenheit scale: 180/100 or 9/5.  So, basically, we are performing the opposite operation depending on which temperature scale we start with.  To convert from Celsius to Fahrenheit, we first multiply the Celsius temperature by our 9/5 from earlier.  Second, you must add 32 degrees.  


Let's try some examples of converting from Fahrenheit to Celsius:


1.) 67.3 degrees F = how many degrees C?
2.) 45.0 degrees F = how many degrees C?
3.) 89.1 degrees F = how many degrees C?


Solutions:


1.) Subtract 67.3-32.0 = 35.3.  Now, multiply this by 5/9.  35.3 x 5 = 176.5 / 9 = 19.61 degrees C, rounded to the nearest hundredth.  


2.) Subtract 45.0-32.0 = 13.  Now, multiply this by 5/9.  13 x 5 = 65 / 9 = 7.22 degrees C, to the nearest hundredth.


3.) Subtract 89.1-32.0 = 57.1.  Now, multiply this by 5/9. 57.1 x 5 = 285.5 / 9 = 31.72 degrees C, to the nearest hundredth.


Let's try some examples of converting from C to F now:


1.) 80.7 degrees C = how many degrees F?
2.) 12.7 degrees C = how many degrees F?
3.) 56.4 degrees C = how many degrees F?


Solutions: 


1.) Multiply 80.7 x 9/5 = 145.26.  Now, add 32 degrees.  145.26 + 32 = 177.26 degrees F.


2.) Multiply 12.7 x 9/5 = 22.86.  Now, add 32 degrees. 22.86 + 32 = 54.86 degrees F.


3.) Multiply 56.4 x 9/5 = 101.52.  Now, add 32 degrees.  101.52 + 32 = 133.52 degrees F.


The following links are useful for further explanation and self-converter of the temperature scales and conversions:


1.) Temperature Scale Converter: Should only be used to check your answers
2.) 3 Different Temperature Scales Used Today








     

Time: Subtracting Weeks and Days

Hello,

In our last post we learned how to add weeks and days together.  Today we are going to learn how to subtract weeks and days.  It is basically the opposite of adding weeks and days.  To add weeks and days, we added the weeks and days together, and then we subtracted 7 from the number of days if it was greater than or equal to 7, and then we increased the weeks by 1.  We would repeat this process if the days were still 7 or greater. 

For subtraction we are going to follow these steps:

1.) Subtract the number of weeks from one another and then subtract the number of days from one another; first, you must check if the second step holds:
2.) If the number of days is less than what you originally started with, you must subtract 1 from the original number of weeks, and then add 7 to the original amount of days.
3.) Once again, subtract the weeks and days. 

Examples:

1.) 6 weeks, 8 days - 5 weeks, 3 days = ?
2.) 5 weeks, 4 days - 3 weeks, 9 days = ?
3.) 7 weeks, 2 days - 2 weeks, 6 days = ?

Solutions:

1.) Since the number of days being subtracted (3) is less than the original days (8), we do not need to worry about our steps.  So, we subtract normally.  6 weeks - 5 weeks = 1 week.  8 days - 3 days = 5 days.  So, our final answer is 1 week, 5 days.

2.) Since the number of days being subtracted (9) is greater than the original amount of days (4), we must follow our steps above.  First, we must subtract 1 from our original amount of weeks, which was 5.  So, now we have 4 weeks.  Now, we add 7 to our original amount of days (4).  4 days + 7 days = 11 days. Now, we can proceed with subtracting.  4 weeks - 3 weeks = 1 week.  11 days - 9 days = 2 days.  So, our final answer is 1 week and 2 days.

3.) Since our number of days that we are subtracting (6) is greater than our original amount of days (2), we must subtract 1 from our original amount of weeks (7-1 = 6 weeks).  Then, we must add 7 to our original amount of days (2 + 7 = 9 days).  Now, subtract normally.  6 weeks - 2 weeks = 4 weeks.  9 days - 6 days = 3 days.  So, our final answer is 4 weeks, 3 days. 

It is confusing at first, but once you practice, I know you'll be able to do it!

The following are links that reiterate how to subtract weeks and days, which will hopefully help you:

1.) How to subtract weeks and days:explanation and example
2.) Subtract weeks and days to a date calendar

Time: Adding Weeks and Days

Hello,

In our last post, we learned about the number of days in each month and how to convert from weeks to days and days to weeks.  In our post today, we are going to learn how to add days and weeks together.

Let's review: 1 week = how many days? If you are thinking 7, you are correct!
Let's go over the rules for days and weeks addition:

1.) Add your days together.
2.) Add your weeks together.
3.) If your days add up to 7 or greater, you will subtract 7 from your days, and then increase your weeks by 1.
4.) If the amount of days is still 7 or greater, then you will repeat step 3. 


Remember that step 3 is the key!

Let's try some examples: Add the following weeks and days.

1.) 2 weeks, 6 days + 3 weeks, 2 days = ?
2.) 1 weeks, 4 days + 9 weeks, 1 day = ?
3.) 7 weeks, 5 days + 4 weeks, 7 days = ?
4.) 3 weeks, 8 days + 8 weeks, 3 days = ?
5.) 6 weeks, 14 days + 2 weeks, 2 days = ?

Solutions:

1.) Add the weeks together first, and then the days together.  2 weeks + 3 weeks = 5 weeks; 6 days + 2 days = 8 days.  Since your number of days is greater than or equal to 7, you're going to subtract 7 from your amount of days (8-7 = 1) and then add 1 to your weeks (5 + 1 = 6).  So, you're final answer is 6 weeks and 1 day.

2.) 1 week + 9 weeks = 10 weeks; 4 days + 1 day = 5 days; so, since your amount of days is less than or equal to 7, you can stop right there, and you're done.  So, you're final answer is 10 weeks and 5 days.

3.) 7 weeks + 4 weeks = 11 weeks; 5 days + 7 days = 12 days; so, here since we have 12, we must subtract 12-7 days = 5 days.  Then, we must add 1 to our 11 weeks = 12 weeks.  So, our final answer is 12 weeks and 5 days.

4.) 3 weeks + 8 weeks = 11 weeks; 8 days + 3 days = 11 days; so, we must subtract 11 days - 7 = 4 days, and then we must add 1 to our 11 weeks = 12 weeks.  So, our final answer is 12 weeks and 4 days.

5.) 6 weeks + 2 weeks = 8 weeks; 14 days + 2 day = 16 days; we must subtract 16 days - 7 = 9 days, and then add 1 to our 8 weeks = 9 weeks.  We must continue because 9 days is still greater than 7.  So, we take 9 days - 7 = 2 days, and then add 1 to our 9 weeks = 10 weeks.  So, our final answer is 10 weeks and 2 days.

The first link below reiterates how to add weeks and days; it has a practice at the bottom of the webpage; the second link is more for fun--you can add and subtract weeks and days from a certain date.  This is useful if you do not have a calendar around to find the date, and it takes less time.

1.) Explanation of how to add weeks and days with an example
2.) Adding and Subtracting weeks and days to a date calendar

I hope this helps!

Time: Days in a Month; Time: Weeks to Days

In our last post, we learned about different conversions of seconds, minutes, and hours.  Today, we are going to learn about two things: days in each month and converting weeks to days and vice versa. 


To memorize how many days are in each month, we will learn a saying to help us remember. The saying goes like this: 


30 days has September, April, June, and November.  All the rest have 31, except February, which has 28, or 29 if it is a leap year.


It is that easy!


So, just to confirm, we will list the number of days in each month:


January:  31
February: 28 or 29
March: 31
April: 30
May: 31
June: 30
July: 31
August: 31
September: 30
October: 31
November: 30
December: 31


Now, we are going to learn how to convert from weeks to days.  First, we must know that there are 7 days in a week.  To convert weeks back into days, we simply multiply the number of weeks given by 7, since each week has 7 days.  For example, to convert 26 weeks into days, we simply multiply 26 x 7 = 182.  So, 26 weeks = 182 days.  


Let's try a few more examples:


Convert the following number of weeks into days.


1.) 5 weeks = ? days
2.) 17 weeks = ? days
3.) 12 weeks = ? days


1.) 35 days; 5 x 7 = 35
2.) 119 days; 17 x 7 = 119
3.) 84 days; 12 x 7 = 84


Now, we are going to convert from days into weeks.  Since we multiply by 7 to convert from weeks to days, we do the opposite operation to convert days into weeks.  We divide the number of days by 7 to find the number of weeks.  The simplest example is: 7 days = ? weeks?  We simply divide 7 / 7 = 1.  So, 7 days = 1 week.  


Let's try a few more examples:


1.) 49 days = ? weeks
2.) 87 days = ? weeks
3.) 14 days = ? weeks


1.) 49 days = 7 weeks because 49 / 7 = 7
2.) 87 days = 12.43 weeks rounded to the nearest hundredth because 87 / 7 = 12.4285714
3.) 14 days = 2 weeks because 14 / 7 = 2


The following are useful links to help you with both topics we have discussed today:


Note: the first two links should only be used to confirm answers, as they are simply conversion calculators.


1.) Converting weeks to days : calculator
2.) Converting days to weeks: Calculator
3.) Website for learning how to remember the days in each month 

Measuring Time: Hours, Minutes, and Seconds

Hello,

In our previous posts we have learned about fractions, decimals, properties of addition, place values, etc.  We are going to move on to measuring time, and we will start with hours, minutes, and seconds.  In this particular post we will learn how to convert minutes to hours and hours to minutes.  We will also learn how to convert from hours to minutes to seconds and vice versa. 

Basically, you need to know that there are 60 minutes in 1 hour.  So, for example, to convert 45 minutes into hours, you would simply divide 45 into 60.  45/60 = 0.75 when you use long division or your calculator. So, 45 minutes = 0.75 hours.  Let's try an example with converting hours back to minutes.  5 hours is equal to how many minutes?  If you multiply 5 x 60, you will find the amount of minutes.  So 5 hours = 300 minutes.  75 hours is equal how many minutes? 75 x 60 = 4,500 minutes.

As a side note, if we were converting from seconds to minutes to hours, we would not only need to know that there are 60 minutes in 1 hour, but that there are 60 seconds in 1 minute.  For example, 35 hours is equal to how many minutes?  35 x 60 = 2100 minutes.  2100 minutes is equal to how many seconds?  2100 x 60 seconds.  In other words, 35 hours = 2100 minutes = 126,000 seconds.  If we were to reverse our problem and convert 126,000 seconds to minutes and hours, we would proceed with the following computations: 126,000/60 = 2,100 minutes and 2,100/60 = 35 hours.   

Hint: Converting from minutes to hours: divide by 60; converting from hours to minutes: multiply by 60; converting from hours to seconds, multiply by 3600; converting from seconds to minutes, divide by 60; converting from seconds to hours, divide by 3600. 

I know that this seems confusing, but it will be much easier as we practice, I promise.

Let's try these worksheets below; Note that the answers are with the worksheet, but try to do the problems yourself before looking at the answers. 

1.) Worksheet: converting from hours to minutes
2.) Worksheet: converting from minutes to hours
3.) Worksheet: converting from minutes to seconds
4.) Worksheet: converting from seconds to minutes
5.) Worksheet: converting hours, minutes, and seconds; more advanced problems ; Answers to worksheet 5

Look at this website for more practice with conversions, specifically minutes to hours, and hours to minutes :  Go to measurement--time, and click on the fist couple links: More practice with time conversions

Equivalent Fractions

These fractions are equivalent, meaning equal.

Hello,

In past posts, we have discussed fractions; we have learned how to add and subtract fractions, how to convert from improper fractions to mixed numbers, and how to convert from mixed numbers to improper fractions.  Today, we are going to learn about equivalent fractions.  Equivalent fractions represent the same part of something, such as a piece of pizza.  If you cut a piece of pizza in half, you have 2 pieces, while piece is 1 out of the two, or 1/2.  If you cut the pizza into 4 pieces, then 2 of the pieces represent 1/2, and so now you have 2 out of the total 4 pieces, or 2/4.  In other words, 1/2 = 2/4.  Common words to describe equivalent fractions other than 'equivalent to' are 'equal to' and 'congruent to.'  Basically, equivalent fractions multiply the same number to the numerator and denominator to get the new fraction.  1/2 = 2/4 because we can multiply 2 to our numerator, 1, and multiply 2 to our denominator, 2, to get 2/4.  1/2 is also congruent to 3/6 because we can multiply numerator and denominator by 3 to get 3/6.  If we multiplied 1/2 by 4 to the numerator and denominator, what would our equivalent fraction be? Our calculation is 1/2 x 4/4 = 4/8, since when you multiply fractions you just multiply straight across, (numerator x numerator) divided by (denominator x denominator), which we will learn in more detail in another post.

Hint: In order to find equivalent fractions, you must multiply by the same number to numerator and denominator to find your new, equivalent fraction, or you must divide by the same number to numerator and denominator to find your new, equivalent fraction.  Dividing numerator and denominator by the same number to get our equivalent fraction means that we are reducing the fraction, usually in lowest terms.

Let's do some examples of finding equivalent fractions and recognizing equivalent fractions.

1.) 1/3 = ?/6
2.) 5/9 = ?/18
3.) 2/6 = 1/?
4.) True or False. 3/4 = 12/16.
5.) 3/5 = 15/?
6.) 7/10 = 14/?
7.) 4/9 = ?/27
8.) True or False. 1/9 = 7/62.
9.) 4/12 = ?/3
10.) 2/7 = ?/49

Try these examples on your own, and then see the solutions attached here: Answer key to equivalent fractions questions 

For more help with equivalent fractions you can view the chart below, as well as the links below:

Website for understanding equivalent fractions , YouTube video describing equivalent fractions with pictures

Improper Fractions and Mixed Numbers Continued

 Advice of the day:

In our last post, we learned how to convert improper fractions to mixed numbers.  Today we will learn how to convert mixed numbers into improper fractions.  Basically, we are working backwards from what we were doing in our last post.  To review, a mixed number is a whole number plus a fraction, while an improper fraction is where your numerator is larger than your denominator.  In order to learn how to convert mixed numbers to improper fractions, we will go over some examples. 

Examples: Convert the following mixed numbers into improper fractions.

1.) 3 1/2 = ?
2.) 5 2/7 = ?
3.) 7 1/8 = ?
4.) 1 3/4 = ?
5.) 10 1/2 = ?
6.) 2 1/9 = ?
7.) 6 7/8 = ?
8.) 4 2/9 = ?
9.) 8 5/6 = ?
10.) 9 3/5 = ?

Let's do a few together, and then you can try the rest on your own and see the attached answers.   

1.) 3 1/2 = [(2x3) + 1] / 2 = 7/2
2.) 5 2/7 = [(7x5) + 2] / 7 = 37/7
3.) 7 1/8 = [(8x7) + 1] / 8 = 57/8

The pattern is: multiply your denominator by your whole number, add your numerator, and then put that number over your original denominator.

 

Go to this link below to see the solutions to the other problems:  

Solutions to problems 4 through 10

For more help with converting mixed numbers into improper fractions, go to the following links: 

Youtube video with teacher providing an example of how to convert a mixed number into an improper fraction,  Worksheet with 24 practice problems 

I hope this helps! 

Improper Fractions and Mixed Numbers

In our last post, we learned about the different properties of addition.  Today, we are going to be learning how to convert improper fractions to mixed numbers.

We discussed fractions before, which consist of a numerator and denominator.  The only difference between a regular fraction and an improper fraction is that an improper fraction has a numerator larger than the denominator.  For example, 7/2 is an improper fraction because the numerator, 7, is larger than 2, the denominator.  Basically, our goal is to convert  our improper fractions to mixed numbers.  Mixed numbers consist of a whole number and a fraction.  An example of a mixed number is 5 1/2 because 5 is a whole number and 1/2 is a fraction; notice that 1/2 is a regular fraction and not an improper fraction.

How to convert from an improper fraction to a mixed number:  Let's start with an example.  Let's use our 7/2 that we used above.  We first ask ourselves: "How many times does our denominator go into our numerator?"  This will be our whole number part of our mixed number.  Next we subtract how ever many times our denominator goes into our numerator by our numerator.  This will give us our new fraction.  It sounds complicated, but let's try it.  So, how many times does 2 go into 7? 3 times.  So, then we subtract 7 - (2 x 3) and we get 1.  1 is our numerator of our new fraction, and we put that over 2 because that's what we originally started with.  So our mixed number is 3 1/2.

More examples: Convert the following improper fractions to mixed numbers.

1.) 17/4 = ?
2.) 9/5 = ?
3.) 19/6 = ?
4.) 15/2 = ?
5.) 24/9 = ?
6.) 13/8 = ?
7.) 11/3 = ?
8.) 16/5 = ?
9.) 12/5 = ?
10.) 28/9 = ?

1.) 4 goes into 17 four times.  4x4 = 16.  17-16 = 1, so our mixed number is 4 1/4.
2.) 5 goes into 9 once. 5x1 = 5.  9-5 = 4, so our mixed number is 1 4/5.
3.) 6 goes into 19 three times.  6x3 = 18.  19-18 = 1, so our mixed number is 3 1/6.
4.) 2 goes into 15 seven times. 2x7 = 14.  15-14 = 1, so our mixed number is 7 1/2.
5.) 9 goes into 24 two times. 9x2 = 18.  24-18 = 6, so our mixed number is 2 6/9, which can be simplified to 2 2/3 because 6/9 = 2/3 since 3 is divisible by 6 and 9.
6.) 8 goes into 13 once. 8x1 = 8.  13-8 = 5, so our mixed number is 1 5/8.
7.) 3 goes into 11 three times. 3x3 = 9.  11-9 = 2, so our mixed number is 3 2/3.
8.) 5 goes into 16 three times. 5x3 = 15.  16-15 = 1, so our mixed number is 3 1/5.
9.) 5 goes into 12 twice.  5x2 = 10.  12-10 = 2, so our mixed number is 2 2/5.
10.) 9 goes into 28 three times.  9x3 = 27.  28-27 = 1, so our mixed number is 3 1/9.

For more help, visit: for practice with converting improper fractions to mixed numbers, 
 YouTube video on further instruction on how to convert improper fractions to mixed numbers

I hope this helps =)

4 Properties of Addition

Hi boys and girls, I hope that you are having a great day!

Today we will be discussing the different properties of addition that will be useful in your future math classes, perhaps even in college, yes I said college!) as these are properties that will never go away.  There are five properties of addition.  They include: commutative, associative, identity, distributive, and inverse.  I will give the general form of each property in a list below.

1.) Commutative property of addition: a + b = b + a (or) a + (b + c) = (b + c) + a
2.) Associative property of addition: (a + b) + c  = a + (b + c)
3.) Identity property of addition: a + 0 = a = 0 + a
4.) Additive inverse property: a + (-a) = 0
5.) Distributive property of addition: a (b + c) = ab + ac 

Now, these may seem confusing or foreign to you, but all you need to do is memorize them, and examples will help you.  If you look at the commutative and associative properties, they look similar.  However, for the commutative property, what is inside the parentheses will NOT change.  For the associative property, what is inside the parentheses WILL change.  And for the first two properties, you are basically adding two or three numbers, but in a different order.  Properties three and four are pretty self-explanatory; for property three, you are simply interested in adding some number to "x" (x being any number) to always get "x."  In this case, we want zero because any number added to zero gives us zero.  For property four, it is called the inverse property of addition because you are adding the 'inverse' of a number to get zero.  Property five is pretty easy.  You must 'distribute' the 'a' to the 'b' and 'c.'  So you are essentially multiplying 'a' to both 'b' and 'c' and then adding them together.

Examples:  Which property of addition holds for the following?

1.) 5 (4 + 9) = 20 + 45.

2.) 8 + (-8) = 0.

3.) 6 + 1 = 1 + 6.

4.) 7 + (1 + 2) = (7 + 1) + 2.

5.) 6 + (-6) = 0.

6.) 3 + 0 = 0 + 3.

7.) 5 + 6 = 6 + 5.

8.) 0 + 4 = 4 + 0.

9.) (1 + 1) + 5 = 1 + (1 + 5).

10.) 9 (4 + 8) = 36 + 72.

Answers: =)

1.) Distributive
2.) Inverse
3.) Commutative
4.) Associative
5.) Inverse
6.) Identity
7.) Commutative
8.) Identity
9.) Associative
10.) Distributive

Do you understand them?

For more help, go to help with associative, commutative, and distributive properties, properties of addition put into different words, YouTube video with properties of addition

Thanks!



    

Fraction Addition and Subtraction: Problem Type 2

Hello =)

In my previous post, we discussed how to add and subtract fractions with like denominators.  Now we will learn how to add and subtract fractions with unlike denominators, which is not difficult if you practice! Lets proceed with an example: Add 3/4 + 5/12.  First, we simply notice that we have unlike denominators, that is, our bottom numbers are different.  Second, we have to find the least common denominator of the two fractions.  That is, what number can you multiply the one denominator to to get the other denominator, or what number can you multiply to both denominators to get the least common denominator (LCD).  The easiest way to approach this is to list the first few multiples of 4 and 12 and scanning from left to right, we want the smallest multiple that both have.  So, multiples of 4 include: 4, 8, 12, 16, 20.  Multiples of 12 include: 12, 24, 36, 48, 60.  In this example, we are lucky because we have found the least common multiple, which is 12, because scanning from left to right, it is the first common multiple that both have.  So, changing both of our denominators to 12, we now have to find our numerators.  Looking at 3/4, what do we multiply 4 by to get 12? 3.  Now, since we multiplied 4 by 3 to get 12, we have to multiply our numerator, 3, by 3, which is 9.  We are done with our first fraction, and our second fraction does not need to be changed because our denominator is already 12.  So, now our problem is: 9/12 + 5/12 = 14/12. 

Let's try another example.  Subtract the following: 2/5 - 1/8.  We first notice that we have unlike denominators, so we must list the first few multiples of both 5 and 8.  Multiples of 5 include: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, ...  Multiples of 8 include: 8, 16, 24, 32, 40, 48, 56, 64, 72, ... If you notice, there is a common multiple of 40 for both.  Hint: Once you have been practicing with these problems and you cannot think of a common multiple of each of your denominators readily, then just multiple your denominators together, and use that as your least common denominator.  The only disadvantage is that you may have to simplify your answer at the end because you did not choose a smaller multiple.  Okay, now that I gave you that hint, we can proceed with our problem =).  So, our first fraction: 2/5 will change into ?/40?  We multiply 5 by 8 to get 40, so we must also multiply our numerator by 8 to get our new numerator: 16.  Now looking at our second fraction, we must multiply our denominator by 5 to get 40, so we must multiply our numerator by 5 to get our new numerator: 5.  Finally, our problem is: 16/40 - 5/40 = 11/40.

Let's do one more example.  Solve 4/15 + 7/3.  If you list your multiples of 15 and 3, you should see that your least common multiple of the two is 15.  Our first fraction stays the same because it already has a 15 for its denominator, but our second fraction must change from 7/3 to ?/15? If you guessed 35/15 you were correct!! =).  Since we had to multiply our denominator by 5 to get 15, we had to multiply our numerator, 7, by 5, which is 35. 

Remember: Whatever you have to multiply to your bottom number by to get the new denominator, you must also multiply to the top.    

For more instruction, watch these video to help you: adding fractions with unlike denominators and
subtracting fractions with unlike denominators
You can also go to this website for help with fractions: subtracting fractions

If you have any questions, do not hesitate to ask!

Fraction Addition and Subtraction: Problem Type 1

Hi, today's post will be a lesson on fractions.  That is, we will learn how to add and subtract fractions with the same denominator.  First of all, we must consider whole numbers.  Every whole number can be written as a fraction.  For instance, 4 can be written as 4/1, and be the same number.  This works for any whole number.  Second of all, lets define fractions.  A fraction consists of a top and bottom number, with the top number known as the numerator and the bottom number known as the denominator.  When adding and subtracting fractions, you may want to keep this in mind.  In order to show you how to go about adding fractions with the same denominator, let me give you an example.  To add 2/7 + 3/7, you first notice that your denominators are the same, which are 7's.  So, all you need to do is add your numerators 2 and 3 together.  So your answer is 5/7.  It's very simple!  How about 1/6 + 3/6? You will add your 3 and 1 and then keep your 6.  So your answer will be 4/6, or if you simplify further, you notice that 2 is divisible by both 4 and 6, and so you can reduce 4/6 to 2/3.  Make sense? 
So, overall, here is the key to adding fractions with the same denominator: Add your numerators and keep your denominator.  Do not add your denominators together.  In order to subtract fractions with the same denominator, you take the same steps as you did to add fractions with like denominators, but you SUBTRACT!  Let's do one example to make sure that you are confident in yourself when you work on these example problems provided at the end of this post.  Tell me what 7/15 - 5/15 is.  All you have to do is subtract 7-5 and keep your denominator since both denominators are the same.  So, your final answer should be 2/15!

Thanks for reading, and hopefully that the following links and worksheet will help you practice and grasp the concept better =)

Fraction practice game
For more info on subtracting and simplifying fractions

Note: For the second link, only read up until reducing fractions.

      

Practice with rounding numbers to the nearest tens, hundreds, and thousands

The last post that I posted had to do with place values.  Rounding is kind of like learning the different place values.  In order to round, you need to know what place value you are talking about.  When rounding, you are basically bumping up to a higher number or bumping down to a lower number.  When rounding, you are approximating, meaning you are not finding an exact answer, but an estimate.  There are two things that you need to remember in order to round numbers to the nearest ten.  First, if the number ends in one through four, you need to round down to the next number that ends in zero.  For example, if you need to round 63 to the nearest ten, you will round down to 60.  Second, if the number ends in five or greater, you need to round up to the next even ten.  For example, if you need to round 48 to the nearest ten, you would round up to 50, which is the next even ten.  To round numbers to the nearest hundred is not much different.  For example, round 671 to the nearest hundred.  You must look at the digit right next to the hundreds place, which is 7.  Since it is greater than 5, you will round 671 to 700, versus 600.  Another example: round 825 to nearest hundred.  Since the digit next to the hundreds place is less than 5, you will round 825 down to 800, versus 900.

Lets go back to rounding to the tens place with these two previous examples.  For the first, to round 671 to the nearest tens place, you would look at the digit to the right of the tens place, which is a 1.  Since it is less than 5, you will round 671 down to 670.  For the second, to round 825 to the nearest ten, you would look at the digit to the right of the tens place, which is 5.  Since it is a 5, you will round 825 up to 830.

Now that we have looked at examples of how to round to the nearest tens and hundreds place, lets look at how to round to the nearest hundreds place.  We will go ahead and do a few examples: 1.) Round 4,564 to the nearest thousands place.  Looking at the previous place value, which is the hundreds place, we see a 5, meaning we will round 4,564 down or up?  We will round 4,564 up to 5,000.  2.) Round 7,340 to the nearest thousands place.  Looking at the hundreds place, we see a 3, meaning we will round down.  So, 7,340 rounded to the nearest thousands place is 7,000.  And just so we are on the same page, what would 7,340 rounded to the nearest hundreds place be?  Looking at the previous place value, we see a 4, meaning we will round down, correct?  Correct.  So, 7,340 rounded to the nearest hundreds place would be 7,300.

For further assistance, you can comment on my post, or you can visit the following links to practice and build confidence in yourself =)

http://www.ixl.com/math/grade-4/rounding

http://www.myschoolhouse.com/courses/O/1/16.asp 

http://www.superkids.com/aweb/tools/math/round/round6.cgi and for the answers to this worksheet, go to: http://www.superkids.com/aweb/tools/math/round/round6_answer.cgi

Place Value Help!

Today, I am posting examples and resources of place values.  Basically, when thinking about place values, you are looking at the individual digits of a number.  Place values include: ones, tens, hundreds, thousands, ten thousands, hundred thousands, etc.  For example, the number 76 has two digits, and each digit is a different place value.  The first digit, 7, is called the tens place.  The second digit, 6, is called the ones place.  Given another example, 5,671, the 5 is called the thousands place, the 6 is the hundreds place, the 7 is the tens place, and the 1 is the ones place.  When talking about money, for instance if you have $56.47, the 5 is the tens place, the 6 is the ones place, the 4 is the tenths place, and the 7 is the hundredths place.  It's easy to get confused because of the "ths" at the end when you have decimals involved, but just remember to add the "ths" if the digit is to the right of a decimal.  You should also remember that after the decimal point, you will have tenths, hundredths, thousandths, ten thousandths, and so on, versus with whole numbers, it starts with ones, then tens, then hundreds, etc.  Let's try one more example.  What place value is the 8 in the following number: 80,457.60?  The 8 is in the ten thousands place.  What about the place value for 6?  The 6 would be the tenths place.  Got it?  =)  If you need help or want more practice the following resources will definately help!  There are free place value worksheets at http://www.softschools.com/math/worksheets/placevalue_worksheets.jsp.  There is also another worksheet with answers for practice with place values through thousands.  If you go to

http://www.softschools.com/grades/4th_grade/math/, click on find place value of a number under 4th grade math games, and this will be a fun way to practice more.  Last, but not least, if you go to http://www.ixl.com/math/grade-4, click place values under the 1st category called Number Sense.

4th grade math practice with decimals continued

Learning how to multiply and divide decimals is a bit different from adding and subtracting decimals, but it is easy once you practice!  When adding and subtracting decimals, we brought the decimal point straight down where our answer would be after adding place holders to help us.  When multiplying decimals, you would first multiply your numbers together like you normally would.  When finished, you then have to count how many numbers there are after each decimal point.  Then, you count from the right of your answer to the left however many digits you counted after your decimals, and place your decimal point in your answer.  For example, to multiply 16.58 x 37.2, we would first multiply the numbers together and forget about the decimal points.  So 1658 x 372 = 616776.  Now you look at your original problem and count the number of digits after your decimal points: 16.58 x 37.2.  There are three digits after the decimals.  So we take our answer we got, 616776 and count from the right to the left 3 digits.  So, now our final answer is 616.776.  For a video on how to multiply decimals, go to http://www.youtube.com/watch?v=EDd9xaGNP_Q.  To divide decimals, you first need to use your long division skills! (yes, I know you may hate long division, but we will get through this =)).  We will review an example of a long division problem to begin.  Use long division to divide 54.0 / 2.5.  Which number goes on the outside and inside of the division bar?  The number on the bottom of the fraction, or in our case to the right after the slash, goes on the outside of the division bar.  And our numerator, or number to the left of the slash, always goes on the inside.  So, looking our decimal points, we must move those decimal points to the right.  For our number outside the division bar: 2.5, we would only have to move our decimal over once to the right to make a whole number.  Since we moved the decimal over once in 2.5, we are going to move our decimal over once in 54.0.  Important to note: however many times you move your number's decimal outside the division bar, you must move your number's decimal inside the division bar to the right the same amount of times.  In our case, we would move the decimal in 2.5 over once to the right to make 25. .  Now, in the same manner, move the decimal in 54.0 to the right once to make 540. .  Now we may begin to divide since we got rid of our decimals.  We must find how many times 25 goes into 54, meaning 25 multiplied by what is closest to 54?  25 goes into 54 twice because 25 x 2 = 50, which is closest to 54.  Now write the 2 above the 4, and write 50 underneath 54, then subtract.  Now, bring your zero down and proceed.  Now our question is,  how many times does 25 go into 40?  25 goes into 40 once, so now place your 1 above your zero in 540.  Next, write your 25 underneath your 40 and subtract.  You should get 15.  Now, we must add a place holder to our 540 and bring that down to our 15, making it 150.  Then, we must find how many times 25 goes into 150.  You will find that 25 x 6 = 150 exactly.  Because of this, we are done dividing.  Now we must worry about our decimal in our final answer.  All you have to do is move your decimal up from 540, so our final answer is 21.6.  You can always check your answer by multiplying 21.6 x 2.5.  For more practice, you can visit the video: http://www.youtube.com/watch?v=AZ6fyQDVqEE.  And for more practice with long division, visit: http://www.softschools.com/math/division/long_division/.

These are examples of dividing and multiplying decimals:

                             

4th grade math practice with decimals

Learning how to add, and subtract decimals is as easy as one, two, three!  The first step in solving an addition problem with decimals is to line up the decimals.  For example, if you have to add a number where one number lies after its decimal to another number where two numbers lie after its decimal, then you would simply put a place holder, or a zero, next to your first number's digit that lies after its decimal.  It may sound difficult, but here is an example.  To add 125.2 + 136.58, you would first line the decimals up and then place a zero next to the .2 in the first number, so that you can keep all of your columns nice and neat.  In other words, you will add 125.20 + 136.58.  Your answer should be 261.78.  For more practice, you can complete this worksheet at the following website: http://www.education.com/worksheets/fourth-grade/math/.  The title of the worksheet is called "Dizzy Over Decimals: Addition # 1."  To subtract decimals, you do the exact same procedure as you did before to add decimals.  For example, to subtract 458.961 - 62.54, you would simply add a place holder to your second number: 62.540.  If it helps to place a zero before the 6 in your first number, you can do so: 062.540.  Next, you would drop your decimal down to your answer and start subtracting.  Your answer should be 396.421.  For a video of how to add and subtract decimals, go to http://www.youtube.com/watch?v=Mn3BKVuWVP4.  I hope this helps!

These are examples of adding and subtracting with decimals for further assistance: